编者按:
样本量对任何一项临床研究来说都十分重要,尤其是在微生物组研究中。考虑到微生物组的个体差异性,确定临床微生物组研究所需的样本尤为关键。过少的样本量难以帮助我们发现差异,而过多的样本量意味着巨大的研究成本。那么究竟需要多少样本量?如何进行合理的估算呢?
今天,我们特别编译了发表在 Gastroenterology 杂志上题为'Microbial Diversity in Clinical Microbiome Studies: Sample Size and Statistical Power Considerations'的文章。希望本文能够为相关的产业人士和诸位读者带来一些启发和帮助。
临床研究,从观察性病例报告到随机对照试验,通常需要建立明确且可检验的研究假设。计算把握度(power calculation)和估算最小样本量,是充分检验研究假设和得出可以超出研究样本范围、能进行推广的有统计学意义结论的重要前提条件。并且还需要根据研究人员可以接受的误差范围,设定置信区间。
需要注意有两类错误,Ⅰ 型错误指实际不存在效果,却错误地得出假阳性结果;Ⅱ 型错误指实际存在效果,却错误地得出假阴性结果。在诊断术语(diagnostic terms)中,Ⅰ 型错误代表缺乏特异度,Ⅱ 型错误代表缺乏敏感度。
临床研究中,Ⅰ 型错误(α)错误水平一般为 5%,Ⅱ 型错误(β)为 20%或 10%。两组人群进行比较时,计算把握度有助于确定避免出现 Ⅱ 型错误所需的最少样本量,换句话说,研究敏感度较高,有助于发现两组之间实际存在的差异。
因此,最终的目的就是招募足够的受试者,在具有充分把握度的前提下,得出差异性结论。但是,也没有必要招募过多受试者,避免资源浪费或给患者带来不必要的不适或痛苦。
通常临床研究中的研究假设主要包括有临床意义的参数、生物标志物或治疗(“自变量”或“预测”变量)与临床结局或结果(“因变量”)的关系。例如,血浆中的促炎蛋白浓度与疾病预后是否存在相关性?口服一种新型降压药物是否可以降低平均收缩压?
确定了 Ⅰ 型和 Ⅱ 型误差的可接受的错误水平,我们就必须确定自变量变化对因变量的影响大小(effect size)。在临床研究中,一个特别关键的因素是自变量是否能够对因变量产生不仅在统计学上有意义,同时还具有临床意义的影响。

通过微生物相关生物标志物预测临床结局是目前的研究热点,也是非常有前景的研究领域1~3。
人类肠道中的微生物对健康的重要性逐渐引起人们的关注。人类肠道内有多种微生物,包括细菌、古菌、真菌、真核生物和病毒(包括噬菌体、攻击细菌或古菌的病毒等)。这些微生物统称为 microbiota,它们的基因被称为 microbiome4。
肠道微生物多样性与影响人类健康的生物变化存在着直接或间接的关联5。因此,深入了解微生物多样性对健康的影响,是临床专业研究的需要拓展的一个研究领域,涉及从精神病学到胃肠病学等一系列学科6。
例如,炎症性肠病疾病的动态变化以及在不同采样部位存在的差异性,都会产生不同的微生物组结果7,8。回肠采集的活检样本预测能力最高,其次是直肠活检和粪便样本。然而,有研究表明,将单个受试者多次粪便样本混合,其预测有效性与回肠活检样本(收集困难,费用昂贵)基本一致9。
综上,微生物组的时间变异性,提示其可能是炎症性肠病甚至其它疾病的潜在标志物。
由于微生物的这些潜在应用,关于微生物组的研究迅速增长,包括学术界、社会企业甚至临床研究机构。因此,成功实施临床微生物组学研究,有几个步骤至关重要。
最近的综述中详述了实验设计中的影响因素,如样品采集和储存11,样品制备方法4和分析方法12,13。本文通过列举两个案例,来阐述一个简单微生物组研究所需的受试者样本量和把握度计算方法。
为了简便起见,本文中给出的两个例子均采用同一个研究 QIITA。
例一中,采用了一种称为 Faith's PD14 的方法来评估微生物多样性,该方法将微生物的系统进化树作为因变量。PD 描述了单个样本中微生物群落的多样性(α 多样性),同时也考量了这些微生物的系统发育结构。
例二中,采用了一种称为 UniFrac(β多样性)的距离度量法,比较了3种不同临床表型/类别微生物多样性之间的差异15。UniFrac 也使用了系统进化树;并通过对菌群的 α 和 β 多样性进行测定,取代了单纯利用已知的分类列表。
相比较之下,单纯利用已知的分类列表的证据力度相对较弱,因为该方法忽略了微生物群之间的相互作用(例如,分类列表法中认为大肠杆菌和沙门氏菌的不同之处,跟它们与芽孢杆菌不同是一样的)。
例一用于推动临床生物标志物研究的标准样本量的计算,而例二则解决的是多元模型和距离矩阵的复杂性。
一项临床研究对两组不同克罗恩病(CD)患者的微生物群落多样性进行了比较。虽然克罗恩病病灶位置一致,但在整个病程中其表型可能有明显差异16。
研究假设为:假设肠道微生物群落差异与克罗恩病表型有关。
为检验该假设,研究将对患有克罗恩病非狭窄非穿透型(B1 型)和患有狭窄型(B2 型)或穿透型(B3 型)的患者进行比较。为了确定每组能够检测出微生物多样性差异的最少受试者人数,研究特意咨询了当地的统计学专家。为进行样本量计算,统计学家可能会问到以下几个问题:
一项可能的研究设计,需要连续纳入确诊为克罗恩病 B1 或 B2/B3 型的患者(B1组vs B2/B3组)。为了方便起见,本文假设所有表型招募难易程度基本相同,推荐组间受试者比例为 1:1。每次随访,患者需要提供一份粪便样本,采用 16S rRNA 标记基因法对菌群群落进行分析。
需要注意的是,对于初步探索研究来说,标记基因法完全可以检验研究假设;但是如果关注的是某一个特殊菌株或功能基因和通路,那么就需要完全不同的测序技术,那么就必须对额外获取数据成本(包括过程成本和数据分析成本)与获得信息是否对等做出权衡。
在上述案例中,研究中克罗恩病患者肠道菌群 α 多样性分布未知,但是存有一项相似的研究,并且该研究及其数据已经公开17。该分析结果表明,100 个 B1 型克罗恩病患者的 PD(用于计算菌群 α 多样性参数之一)呈正态分布。PD 的平均值和标准差分别为 13.5 和 3.45(见图1)。
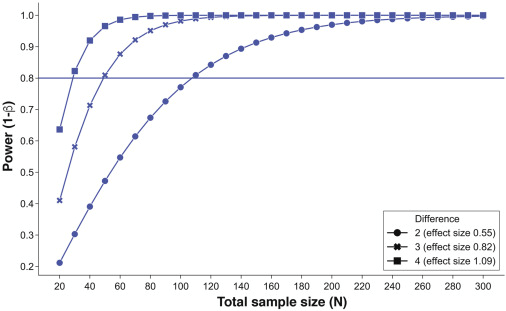
图1:标准样本量计算。确定在 B1 组和 B2/B3 组患者肠道菌群 α 多样性(Faith PD)存在显著差异,且在3个效应值(PD差异为2、3、4,相当于 Cohen D 为 0.55、0.82和1.09),把握度为 80%。
图表结果显示,尽管在样本量为 20 时即可得出显著性差异(α<0.05),但是实际能够检验出这种差异的概率小于 30%。因此,按照80%把握度检验各组间菌群多样性的差异,按照差异度 0.55 计算,最少需要患者人数为 110 人(每组 55 人)。
需要注意的是,图示说明了为什么把握度不高的研究也会发表:如果 10 个不同的研究者,都完成了 20 个样本量的研究,那么至少有一个得出阳性结果的概率大于 97%。而设计一项新的研究,与一项已经发表但把握度不足的研究比较,更有可能会产生阴性结果。
接下来,需要确定多大的差异才是有临床意义的(样本量足够大时,即使很微小的差异也可能检验出统计学差异,但是这个差异无任何临床意义)。因此,我们需要计算能检验出组间有意义差异的样本量。但是通常情况下,多大的差异才有临床意义,答案是未知的。
比如,假设将 PD 单位的下降作为指标,那这个下降程度到底有多大影响呢?已知分布的标准差为 3.45,单位下降程度 Cohen’s D 效应值(标准差的差异)为 0.29。目前的共识为,标准差差异小于 0.4 时,代表影响相对较小,提示在初始计算时选择相对较大的差异更适宜。
事实上,在本研究中,与未接受抗生素治疗组患者相比,接受抗生素治疗组患者 PD 下降了 1.5 个单位,差异有统计学意义(P<0.001)。因此,1.5 单位 PD 差异是适宜的。
假设研究者需要在组间检测出 2 单位 PD 的差异(μ2-μ1)。基于本研究中 PD 分布,利用已知差异水平和样本量拟合把握度曲线(见图1)。从图中可以看出,效应值为 0.55 时,仅需要 10 名患者就可以观察显著差异(如深蓝色圆圈所示),但此时的统计学把握度不足 30%。从统计诊断学角度讲,类似于某项检验特异度较高,但是敏感度很低,因此无法检验出实际的影响(即,当 H0 假设为错误时,拒绝 H0 假设)。
一般情况下,大部分研究采用的统计学检验水平为 5%,把握度为 80%。就本研究而言,想要检验出两组受试者 2 个单位肠道菌群 α 多样性差异,建议纳入 110 名患者(每组 55 人)。
值得注意的是,招募 55 名具有特殊疾病表型患者的组织工作极具挑战性,如果时间允许的话,建议提前开展一些预实验。此外,如果将药物、年龄、饮食或体重指数等因素纳入考虑范畴,研究将变得愈加复杂。在这样的情况下,应该选择满足较大的效应值。
显而易见,在上述例子中, 50 名患者的总样本量可能就可以检验出 0.8 的效应值(即相当于 3 个 PD 单位的差异),但这样的缺点是可能会遗漏掉真实存在但影响较小的作用。
例一说明了从菌群 α 多样性来看,其与大多数临床研究中标准样本量的计算公式相一致。而检验菌群 β 多样性研究假设所需样本量的计算,受到患者分组或疾病临床表型和其他因素的影响。此处,需要合适的度量标准,计算样本矩阵间的成对距离。
样本间距离反映的是微生物群组成(两组微生物群组成一致时,度量值趋向于 0)和组间差异,以说明微生物群本身的差异(而不是微生物群种类数量不一致)与特殊临床表型相关。
自变量依然是疾病临床表型,因变量为微生物样本的距离,检验假设 H0 为从同一组随机抽取一对样本的距离与从不同分组随机抽取一对样本的距离相同。
本文将计算检验出 B1 和 B2/B3 表型患者微生物成对距离差异有统计学意义所需的最小样本量。
研究中将采用基于系统发育的β多样性(unweighted UniFrac)来检验假设。如果按照之前的逻辑,我们会发现 B1 表型患者菌群成对距离分布近似正态分布,UniFrac 平均值为 0.55±0.08;而 B1 表型和 B2/B3 表型患者之间成对距离校对较大,UniFrac 平均值为 0.60±0.07。
从图 2 可以看出,达到显著性为 5%、统计效力为 80%的中等效应值(0.60)所需患者总数约为 100 例(每组 50 例)。

图 2 两组菌群成对距离显著性检验相关样本量计算。(左图)该图可用于确定肠道菌群 β 多样性显著性检验的受试者总数,类似于例一中不同检验水平对应不同的把握度。(右图)两组直方图分别表示 B1 表型成对距离的分布、B1 和 B2/B3 表型成对距离的分布。结果显示,与 B1 和 B2/B3 表型间成对距离相比,B1 表型内成对距离短,且异质性较弱。
本文所述方法适用于在单个时间点,以及在有初步数据的情况下测量微生物多样性的研究。然而,对于缺失初步数据或者小型预实验,综合考虑研究的可行性和不同的效应值(根据较大的标准差计算得到)进行预估是十分必要的。另外,如果目标参数呈非正态分布,则需要采用不同的分析方法19。
同样,如果是重复测量或纵向研究,样本量和把握度的计算则相对复杂一些,因为必须明确重复测量的标准差和相关关系(相关类型)20。关于检验特殊微生物的显著差异研究的样本量和把握度计算则更具挑战性,Morton 等人对此进行了广泛的讨论21。
不过,在上述的两种情况中,想要通过查询现有数据预测效应值的模型都仍然需要进一步的研究。

总之,确定临床微生物组学研究所需的最低样本量,目前还是一个悬而未决的问题。
我们认为,通过选择适用于微生物群 α 多样性和 β 多样性的度量指标,并使用已发布的相关研究中的度量指标的分布作为评估样本量的第一步。这样,无论是假设验证性研究还是探索性研究,在已知差异度和检验水平的情况下,都能得到适宜的把握度。
需要强调的是,本文所讨论的挑战是如何利用多样性指标在特定群体中的分布来设计一项可能得出有意义结论的研究。这与根据患者或受试对象个人基本度量指标数据进行分组不同。
例如,在上述例子中,根据炎症性肠病表型定义,测量单个样本的 PD 值并不足以对患者进行表型分类。因此,即便各组肠道菌群 PD 值差异很明显,但是 PD 值不能作为炎症性肠病表型用于临床检验。
因此,评审专家和机构评审委员会一般都会要求提交详细的研究方案及详细的计划细节,确保研究纳入了足够的受试者,以便得出有意义的临床/生物学结论。
为此,我们尝试将标准临床研究参数中统计学把握度计算方法,与临床微生物组学研究中常用的 2 个独立变量指标——α 和 β 多样性进行融合。
微生物组数据(包括基因序列、元数据 17 和计算机资源)的可及性,对于如何以最低成本检验研究假设非常重要。我们预计,随着储备的研究数量越多,利用微生物组数据计算的把握度的工具就将越有效,对整个实验设计和临床微生物组研究结果的解释就越有利。
参考文献:
(滑动下方文章查看)
1. Doherty MK, Ding T, Koumpouras C, et al. Fecal microbiota signatures are associated with response to ustekinumab therapy among Crohn’s disease patients. MBio 2018;9.
2. He Y, Wu W, Zheng HM, et al. Regional variation limits applications of healthy gut microbiome reference ranges and disease models. Nat Med 2018; 24:1532–1535.
3. Pascal V, Pozuelo M, Borruel N, et al. A microbial signature for Crohn’s disease. Gut 2017; 66:813–822.
4. Debelius J, Song SJ, VazquezBaeza Y, et al. Tiny microbes, enormous impacts: what matters in gut microbiome studies? Genome Biol 2016;17:217.
5. Lozupone CA, Stombaugh JI, Gordon JI, et al. Diversity, stability and resilience of the human gut microbiota. Nature 2012; 489:220–230.
6. Knight R, Callewaert C, Marotz C, et al. The microbiome and human biology. Annu Rev Genomics Hum Genet 2017;18:65–86.
7. Gevers D, Kugathasan S, Denson LA, et al. The treatmentnaive microbiome in new-onset Crohn’s disease. Cell Host Microbe 2014;15:382–392.
8. Halfvarson J, Brislawn CJ, Lamendella R, et al. Dynamics of the human gut microbiome in inflammatory bowel disease. Nat Microbiol 2017;2:17004.
9. Vazquez-Baeza Y, Gonzalez A, Xu ZZ, et al. Guiding longitudinal sampling in IBD cohorts. Gut 2018; 67:1743–1745.
10. Zaneveld JR, McMinds R, Vega Thurber R. Stress and stability: applying the Anna Karenina principle to animal microbiomes. Nat Microbiol 2017;2:17121.
11. Vandeputte D, Tito RY, Vanleeuwen R, et al. Practical considerations for large-scale gut microbiome studies. FEMS Microbiol Rev 2017;41:S154–S167.
12. Nearing JT, Douglas GM, Comeau AM, et al. Denoising the denoisers: an independent evaluation of microbiome sequence errorcorrection approaches. PeerJ 2018; 6:e5364.
13. Allaband C, McDonald D, VazquezBaeza Y, et al. Microbiome 101: studying, analyzing, and interpreting gut microbiome data for clinicians. Clin Gastroenterol Hepatol 2019;17:218–230.
14. Faith DP, Baker AM. Phylogenetic diversity (PD) and biodiversity conservation: some bioinformatics challenges. Evol Bioinform Online 2007;2:121–128.
15. Lozupone CA, Knight R. The UniFrac significance test is sensitive to tree topology. BMC Bioinformatics 2015;16:211.
16. Louis E, Collard A, Oger AF, et al. Behaviour of Crohn’s disease according to the Vienna classification: changing pattern over the course of the disease. Gut 2001; 49:777–782.
17. Gonzalez A, Navas-Molina JA, Kosciolek T, et al. Qiita: rapid, webenabled microbiome meta-analysis. Nat Methods 2018; 15:796–798.
18. Kazis LE, Anderson JJ, wMeenan RF. Effect sizes for interpreting changes in health status. Med Care 1989;27:S178–S189.
19. Cundill B, Alexander ND. Sample size calculations for skewed distributions. BMC Med Res Methodol 2015;15:28.
20. Guo Y, Pandis N. Sample-size calculation for repeated-measures and longitudinal studies. Am J Orthod Dentofacial Orthop 2015; 147:146–149.
21. Morton JT, Marotz C, Washburne A, et al. Establishing microbial composition measurement standards with reference frames. Nat Commun 2019; 10:2719.
原文链接:https://www.gastrojournal.org/action/showPdf?pii=S0016-5085%2820%2930068-8
作者|Rob Knight团队
编译|ninety
审校|617
编辑|晴晴大人